En general, una matriz es un conjunto ordenado en una estructura de filas y columnas. Los elementos de este conjunto pueden ser objetos matemáticos de muy variados tipos, aunque de forma particular, trabajaremos exclusivamente con matrices formadas por números reales. Normalmente las matrices son designadas por letras mayúsculas. Los elementos de una matriz se identifican por la fila y la columna que ocupan. Así, designaremos por a32 el elemento que está situado en la tercera fila y segunda columna de la matriz A.
Nota: Videos de algunos temas al final.
domingo, 11 de octubre de 2009
3.1 DEFINICIÓN DE MATRIZ
jueves, 24 de septiembre de 2009
2.4 Metodos De Solución De Un Sistema De Ecuaciones Lineales (Gauss- Jordan, Eliminación Gaussiana).
METODO DE ELIMINACION GAUSSIANA
El método de eliminación Gaussiana indica cómo se puede llevar una matriz dada a su forma escalonada reducida. Las difrenetes etapas del método se explicarán con un ejemplo particular. Supóngase que tiene un sistema de ecuaciones de cuatro incognitas
3×3–2×2+x1+x0=1
x3-x2-x1–3×0=0
2×3+x2+2×1+4×0=5
2×3–4×2+x1+2×0=4
Esto nos quedara entonces:
Se hace qu el primer elemento de la primera linea (L1) sea 1. Esto es posible multiplicando por 1/3 tal linea. Se obtiene la matriz
Esto nos queda:
Ahora se elininara el primer numero de L2. Esto se hace Multiplicando L1 por −1 y sumandocelo a L2 respectivamente.
Queda así:
(−1)(1)=−1+1=0, (−1)(−2/3)=2/3+(−1)=−1/3, (−1)(2/3)=−2/3+(−1)=−5/3, (−1)(1/3)=−1/3+(−3)=−10/3, (−1)(1/3)=−1/3+0=−1/3.
L2 se multiplica por −3 para hacer 1 el segundo numero de L2
Esto nos da
multiplicando por −3 a L2 (−3)0=0, (−3)(−1/3)=1, (−3)(−5/3)=5, (−3)(−10/3)=10, (−3)(−1/3)=1.
Para eliminar el primer mun de L3 se multiplica L1 por −2 y se suma a L3 respectivamente
queda de la siguiente manera
Para eliminar el segundo numero de L3 se multiplica L2 por −7/3 y se suma a L3 respectivamente
2.3 Interpretación geométrica de las soluciones.
En términos geométricos es el estudio de las posiciones relativas de dos planos, casos que se presentan:
■ Planos paralelos. Sin puntos comunes, cuando el sistema sea incompatible.
Cada ecuación representa un plano en el espacio tridimensional. Luego se trata de estudiar la posición relativa de tres planos en el espacio. Las soluciones del sistema son geométricamente los puntos de intersección de los tres planos, los casos son:
▲ Un punto único. Sistema compatible determinado.. Los tres planos se cortan en P.
p
• Una recta. Son soluciones todos los puntos representativos de la recta común. Sistema compatible indeterminado con un grado de libertad.
Los planos se cortan en r.
▼ Un plano. Los planos son coincidentes. El sistema es compatible indeterminado con dos grados de libertad.
◄ Ningún punto. El sistema es incompatible. Esta situación se presenta geométricamente de distintas maneras. Para estudiar las posiciones relativas de los planos hay que tomarlos de dos en dos.
Se pueden presentar varios casos: Que los planos sean paralelos:
II2
2.2 Clasificación de los sistemas de ecuaciones lineales y tipos de solución.
Los sistemas de ecuaciones se clasifican en 3 tipos: los que tienen infinitas soluciones, los que tienen una solucion y los que no tienen solucion.
=> Tienen soluciones infinitas cuando las rectas del sistema de ecuaciones son paralelas.
=> Tienen una solución cuando las rectas del sistema de ecuaciones se intersectan.
=> No tienen solución cuando estan una sobre otra en las rectas del sistema de ecuaciones.
*Pronto mas inf.
Unidad II. Sistemas de Ecuaciones Lineales
2.1 Definición.
En matemática y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Ecuaciones lineales con más de dos variables.
Para sistemas de ecuaciones lineales con más de dos variables, podemos usar el método de eliminación por sustitución o el método de eliminación por suma o resta (por adición o sustracción).
El método de eliminación por suma o resta es la técnica más breve y fácil de hallar soluciones. Además, lleva la técnica de matrices que se estudia en esta sección.
Cualquier sistema de ecuaciones lineales con tres variables tiene una solución única, un número infinito de soluciones o no tiene solución.
Método de eliminación para resolver un sistema de ecuaciones lineales:
Ejemplo:
Resuelve el sistema:
x + 2y + 3z = 9 …………………………….. (primer ecuación)
4x + 5y + 6z = 24 …………………………. (segunda ecuación)
3x + y - 2z = 4 ……………………………. (tercera ecuación)
Solución:
Suma −4 veces la “primera ecuación” a la “segunda”:
[x + 2y + 3z = 9]−4 → −4x −8y −12z =−36
4x +5y + 6z = 24
0 −3y - 6z = −12
Suma −3 veces la “primera ecuación” a la “tercera”:
x + 2y + 3z = 9
-3y - 6z = −12
-5y - 11z = −23
Multiplica por -(1÷ 3) la “segunda ecuación”:
x + 2y + 3z = 9
y + 2z = 4
-5y −11z = −23
Multiplica por −1 la “tercera ecuación”:
x + 2y + 3z = 9
y + 2z = 4
5y +11z = 23
Suma −5 veces la “segunda ecuación” a la “tercera”:
x + 2y + 3z = 9
y + 2z = 4
z = 3
Las soluciones del último sistema son fáciles de hallar por sustitución. De la “tercera ecuación”, vemos que z= 3. Al sustituir “z” con 3 en la “segunda ecuación”, y + 2z = 4 obtenemos y = −2. Por último, encontramos el valor de “x” al sustituir y = −2 y z = 3, en la “primera ecuación”, x + 2y + 3z = 9 con lo cual x = 4. Por tanto, hay una solución:
x = 4,
y = −2,
z = 3.
lunes, 14 de septiembre de 2009
1.6 Ecuaciones Polinómicas
Una raíz del polinomio p es un complejo z tal que p(z)=0. Un resultado importante de esta definición es que todos los polinomios de grado n tienen exactamente n soluciones en el campo complejo, esto es, tiene exactamente n complejos z que cumplen la igualdad p(z)=0, contados con sus respectivas multiplicidades. A esto se lo conoce como Teorema Fundamental del Álgebra, y demuestra que los complejos son un cuerpo algebraicamente cerrado. Por esto los matemáticos consideran a los números complejos unos números más naturales que los números reales a la hora de resolver ecuaciones.
¿Cómo resolver una ecuación de primer grado? Para la resolución de ecuaciones de primer grado podríamos definir un esquema con los pasos necesarios. Para empezar comenzemos con una ecuación de primer grado sencilla: 9x − 9 + 108x − 6x − 92 = 16x + 28 + 396 Nuestro objetivo principal es dejar sola la x en uno de los terminos, el izquierdo o el derecho.
1. TRANSPOSICIÓN: Lo primero que debemos hacer es colocar los terminos con X en un lado, y los numeros enteros en otro. Para ello, podemos ver que hay algunos números que tendremos que pasarlos al otro termino. Esto lo podemos hacer teniendo en cuenta que: Si el número esta restando (Ej: −6): Pasa al otro lado sumando (+6) Si el número esta sumando (Ej: +9): Pasa al otro lado restando (−9) Si el número esta multiplicando (Ej: •2) Pasa al otro lado dividiendo (en forma fraccionaria) (n/2) Si el número esta dividiendo (en forma fraccionaria) (Ej: n/5) Pasa al otro lado multiplicando (•5) Una vez hemos pasado todos los terminos en nuestra ecuación, esta quedaría así: 9x + 108x − 6x − 16x = 28 + 396 + 9 + 92 Como podrás comprobar todos los monomios con X han quedado a la izquierda del signo igual, y todos los números enteros se han quedado en la derecha.
2. SIMPLIFICACIÓN: Nuestro siguiente objetivo es convertir nuestra ecuación en otra equivalente más simple y corta, por lo que realizaremos la operación de polinomios que se nos plantea Es decir en nuestro caso, por un lado realizamos la operación: 9x+108x-6x-16x Y por otro lado: 28+396+9+92 De forma que nuestra ecuación pasaría a ser esta: 95x = 475
3. DESPEJAR: Ahora es cuando debemos cumplir nuestro objetivo final, dejar la X completamente sola, para ello volveremos a recurrir a la transposición. Es decir, en nuestra ecuación deberíamos pasar el 95 al otro lado, y, como está multiplicando, pasa dividiendo: x = 475 / 95 Comprueba que el ejercicio ya está teóricamente resuelto, ya que tenemos una igualdad en la que nos dice que la x ocultaba el número 475/95. Sin embargo debemos simplificar esto. Resolvemos la fracción (Numerador dividido entre denominador) en caso de que el resultado diera exacto, si nos diera decimal, simplificamos la fracción y ese es el resultado. En nuestra ecuación vemos que si se puede resolver la fracción (475:95=5) por lo tanto x=5 Ya sí hemos resuelto la ecuación, es decir hemos averiguado que el número que x representaba era el 5. Resolución de ecuaciones de primer grado (Problema) Pongamos el siguiente problema: El número de canicas que tengo más tres es igual al doble de las canicas que tengo menos 2.¿Cuántas canicas tengo? El primer paso para resolver este problema es expresar el enunciado como una expresión algebraica: x + 3 = 2x − 2 El enunciado está expresado, pero no podemos ver claramente cuál es el valor de x, para ello se sigue este procedimiento: x + 3 = 2x − 2//Primero se pasan todas las x al primer término y los términos independientes al segundo. Para ello tenemos en cuenta que cualquier expresión pasa al otro término haciendo la operación opuesta. Así obtenemos: x − 2x = − 2 − 3//Que simplificado resulta: − x = − 5//Esta expresión nos lleva a una parte muy importante del álgebra, que dice que si modificamos igualmente ambos términos de una ecuación, el resultado es el mismo. Esto significa que podemos sumar, restar, multiplicar, dividir, elevar y radicar los dos términos de la ecuación por el mismo número sin que esta sufra cambios. En este caso, si multiplicamos ambos términos por −1 obtendremos: x = 5//El problema está resuelto Resolución de ecuaciones de segundo grado Todas las ecuaciones de segundo grado pueden tener como mucho 2 soluciones válidas.Para la resolución de ecuaciones de segundo grado tenemos que distinguir entre tres tipos distintos de ecuaciones: -Ecuaciones de la forma ax2 + c = 0 Este tipo de ecuaciones son las más sencillas de resolver, ya que se resuelven igual que las de primer grado. Tengamos por ejemplo: x2 − 16 = 0//Pasamos −16 al segundo término x2 = 16//Ahora pasamos el exponente al segundo término haciendo la operación opuesta, en este caso raíz cuadrada
La ecuación ya está resuelta
Ecuaciones de la forma ax2 + bx) = 0 Tengamos: 3×2 + 9x = 0//En este tipo de ecuaciones lo primero que hacemos es sacar x factor común de ambas expresiones: x(3x + 9) = 0// Esta expresión es una multiplicación cuyo resultado es 0, por lo tanto una de los factores tiene que ser igual a 0. Así que o el primer factor (x)es igual a cero (esta es la primera solución) o: 3x + 9 = 0 3x = 9.
Por lo tanto, las 2 soluciones válidas para esta ecuación son 0 y 3 -Ecuaciones de la forma ax2 + bx + c = 0 Tengamos por ejemplo la ecuación: x2 + 5x − 6//Para resolver este tipo de ecuaciones utilizamos directamente la siguiente fórmula:
*Por lo tanto para resolver esta ecuación sustituimos las letras por los números:
*A partir de esta fórmula obtenemos que las soluciones válidas para esta ecuación son 1 y −6
domingo, 6 de septiembre de 2009
Leonhard Euler
Leonhard Euler (cuyo nombre completo era Leonhard Paul Euler) fue un respetado matemático y físico. Nació el 15 de abril de 1707 en Basilea (Suiza), y murió el 18 de septiembre de 1783 en San Petersburgo (Rusia). Se lo considera el principal matemático del siglo XVIII y como uno de los más grandes de todos los tiempos.
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática. También se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Euler ha sido uno de los matemáticos más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes. Una afirmación atribuida a Pierre-Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros.»
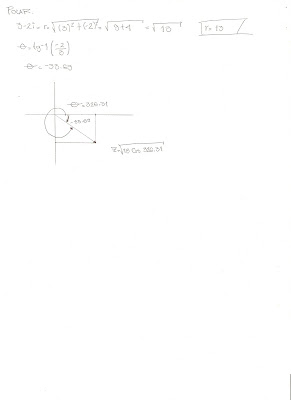
1.3 Potencias De i, módulo o valor absoluto de un número complejo
Valor absoluto. El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión: Si pensamos en z como un punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano. Si el complejo está escrito en forma polar z = r eiφ, entonces |z| = r. Podemos comprobar con facilidad estas tres importantes propiedades del valor absoluto para cualquier complejo z y w. Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio métrico con los complejos gracias al que se puede hablar de límites y continuidad. La suma, la resta, la multiplicación y la división de complejos son operaciones continuas. Si no se dice lo contrario, se asume que ésta es la métrica usada en los números complejos.
Modulo de un vector
Se llama módulo de un complejo a la longitud del vector que lo representa, lo designaremos por ½ Z½ o simplemente por r. Su valor se obtiene por la conocida relación: ½ Z1½ = r = Que es la relación que nos permite determinar la longitud de un vector. Sea Z un número complejo. Explique como determinar Sea Z= a +bi.
La raíz cuadrada del complejo a + bi será otro complejo que llamaremos x + yi: = x + yi = x + yi (])
Elevando ambos miembros al cuadrado y reduciendo términos:
a + bi = x2 + 2xyi + y2i2
a + bi = x2 + 2xyi + y2 (−1)
a + bi = (x2 - y2) + 2xyi
Igualando partes reales y partes imaginarias se forma el siguiente sistema: Despejando “y” en ( ]]] ): Sustituyendo este valor en ( ]] ): Expresando en términos de X2:
Tomamos únicamente el valor positivo, pues es mayor que “a” y x2 no puede ser negativo. Además = S
En la ecuación ( ]]] ) podemos observar que “b” tiene el mismo signo que el producto “xy”. Por lo tanto, si “b” es positivo “x” e “y” serán de igual signo y tendremos que: Para b > 0 Para b < 0
Como los signos que deben tomarse para X e Y deben satisfacer la ecuación 2XY= b, hay que hacer las siguientes consideraciones:
Para b > 0: Las raíces deben ser; ambas del mismo signo: positivas o negativas (+,+), (- , -) Para b < 0: Las raíces, se toman con signos opuestos :(+,-),(-, +)
Modulo de un vector
Se llama módulo de un complejo a la longitud del vector que lo representa, lo designaremos por ½ Z½ o simplemente por r. Su valor se obtiene por la conocida relación: ½ Z1½ = r = Que es la relación que nos permite determinar la longitud de un vector. Sea Z un número complejo. Explique como determinar Sea Z= a +bi.
La raíz cuadrada del complejo a + bi será otro complejo que llamaremos x + yi: = x + yi = x + yi (])
Elevando ambos miembros al cuadrado y reduciendo términos:
a + bi = x2 + 2xyi + y2i2
a + bi = x2 + 2xyi + y2 (−1)
a + bi = (x2 - y2) + 2xyi
Igualando partes reales y partes imaginarias se forma el siguiente sistema: Despejando “y” en ( ]]] ): Sustituyendo este valor en ( ]] ): Expresando en términos de X2:
Tomamos únicamente el valor positivo, pues es mayor que “a” y x2 no puede ser negativo. Además = S
En la ecuación ( ]]] ) podemos observar que “b” tiene el mismo signo que el producto “xy”. Por lo tanto, si “b” es positivo “x” e “y” serán de igual signo y tendremos que: Para b > 0 Para b < 0
Como los signos que deben tomarse para X e Y deben satisfacer la ecuación 2XY= b, hay que hacer las siguientes consideraciones:
Para b > 0: Las raíces deben ser; ambas del mismo signo: positivas o negativas (+,+), (- , -) Para b < 0: Las raíces, se toman con signos opuestos :(+,-),(-, +)
martes, 1 de septiembre de 2009
Unidad I. Números complejos: 1.1.Definición y origen

Mas acerca del tema.
Plano de los números complejos.
Desde un punto de vista geométrico la recta real (recta que representa el total de números reales) puede ser vista como un subconjunto del plano de los números complejos.
Cada número complejo sería un punto en ese plano. Usando las definiciones que siguen, se hacen posibles la suma, la resta, la multiplicación y la división entre estos puntos. Definiremos cada complejo como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), que verifican las siguientes propiedades:
(a, b) + (c, d) = (a + c, b + d)
(a, b) • (c, d) = (ac - bd, bc + ad).
Tal como los hemos definido, los números complejos forman un cuerpo, el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unicode ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales: C no puede ser convertido de ninguna manera en un cuerpo ordenado.
Geometría y operaciones con complejos
Geométricamente, las operaciones algebraicas con complejos las podemos entender como sigue. Para sumar dos complejos z1 =a1 + ib1 y z2 = a2 + ib2, podemos pensar en ello como la suma de dos vectores del plano x-y apuntando desde el origen al punto (a1, b1) y (a2,b2), respectivamente. Si trasladamos (movemos) el segundo vector, sin cambiar su dirección, con lo que su punto de aplicación coincide con el punto final del primer vector; el segundo vector así ubicado apuntará al complejo z1 + z2.
Siguiendo con esta idea, para multiplicar dos complejos z1 y z2, primero medimos el ángulo que forman en sentido contrario a las agujas del reloj con el eje positivo de las x y sumamos ambos ángulos: el ángulo resultante corresponde con el del vector que representa al complejo producto z1 • z2. La longitud de este vector producto viene dada por la multiplicación de las longitudes de los vectores originales. La multiplicación por un número complejo fijo puede ser vista como la una transformación del vector que rota y cambia su tamaño simultáneamente.
Multiplicar cualquier complejo por i corresponde con una rotación de 90º en dirección contraria a las agujas del reloj. Asimismo el que (−1) • (−1) = +1 puede ser entendido geométricamente como la combinación de dos rotaciones de 180º.
Un poco de historia
La primera referencia conocida a raíces cuadradas de números negativos proviene del trabajo de los matemáticos griegos, como Herón de Alejandría en el siglo I antes de Cristo, como resultado de una imposible sección de una pirámide. Los complejos se hicieron más patentes en el Siglo XVI, cuando la búsqueda de fórmulas que dieran las raíces exactas de los polinomios de grados 2 y 3 fueron encontradas por matemáticos italianos como Tartaglia, Cardano. Aunque sólo estaban interesados en las raices reales de este tipo de ecuaciones, se encontraban con la necesidad de lidiar con raices de números negativos. El término imaginario para estas cantidades fue acuñado por Descartes en el Siglo XVII y está en desuso. La existencia de números complejos no fue completamente aceptada hasta la más abajo mencionada interpretación geométrica que fue descrita por Wessel en 1799, redescubierta algunos años después y popularizada por Gauss. La implementación más formal, con pares de números reales fue dada en el Siglo XIX
lunes, 31 de agosto de 2009
Los virus mas importantes de los ultimos 20 años

En los últimos 20 años millones de virus aparecieron en la red y todos ellos nos afectaban de diferentes formas. Algunos reiniciaban nuestros ordenadores, otros borraban nuestros ficheros y otros nos hacían pertenecer a redes de bots para atacar a sitios cuando los crackers así lo indicaran y así se puede continuar durante horas.
Panda antivirus y algunos otros hicieron una lista que además de presentar los virus más importantes de los últimos 20 años tenian su breve descripcion y ejemplo, preocupandose mas bien por lo que iva a venir.
Friday 13 o Jerusalem: Fue creado en el 88 y borraba todos los archivos del ordenador infectado.
Barrotes: El primer virus español conocido. Cuando lograba ingresar al ordenador se mantenía inactivo hasta el 5 de enero y ese día mostraba una serie de barras en la pantalla.
Cascade or Falling Letters: Fue desarrollado en Alemania en los 80's y hacía que todas las letras de la pantalla cayeran como si estuvieran en una cascada.
CIH o Chernobyl: Nació en Taiwán en el 98 y le tomó solamente una semana para reproducirse a través de miles de ordenadores.
Melissa: Uno de los primeros virus que utilizó el famoso mensaje “Aquí tienes el documento que me pediste…no se lo muestres a nadie más ;)” para propagarse.
ILoveYou o Loveletter: Desarrollado en Filipinas en el año 2000 y con el subject ILoveYou infectó millones de ordenadores de todo el mundo, incluso llegó al Pentagono.
Klez: Infectaba sólo a computadoras los días número 13 de meses impares y nació en Alemania en el año 2001.
Nimda: Su nombre es admin si se le lee de atrás hacia adelante y podía generar permisos de administrador en los ordenadores infectados. Se le vio por primera vez el 18 de septiembre del 2001 en China.
SQLSlammer: Infectó a más de medio millón de ordenadores desde el 25 de enero del 2003.
Blaster: Uno de los virus más conocidos de la historia que explotaba una vulnerabilidad de Windows. Fue creado en agosto del 2003.
Sobig: Generó en el verano del 2003 más de 1 millón de infectados y la variante F del mismo era la más dañina.
Bagle: Fue uno de los virus con más variantes de la historia y apareció el 18 de enero del 2004.
Netsky: Otro de los más peligrosos de la historia. Fue desarrollado en Alemania y usaba una vulnerabilidad del Internet Explorer.
Conficker: Uno de los más recientes. Nació en noviembre del 2008 y lo raro era que si tenías el teclado configurado en ucraniano no afectaba al infectado.
Ahora la pregunta es ¿Estamos preparados para lo que viene con nuestras mejores armas?, o acaso dejaremos de utilizar una computadora por miedo a las futuras amenazas...
Suscribirse a:
Entradas (Atom)


































.jpg)






